RESOURCES
量子技術的發展與應用
量子理論由1900年被普朗克(Max Planck)提出后,愛因斯坦(Albert Einstein)、玻爾(Niels Bohr)、海森堡(Werner Heisenberg)、薛定諤(Erwin Schrödinger)等人不斷提出新理論并涌現出相關實驗。這些物理先驅所做的開創性工作和思維變革,顛覆了經典力學對自然界的認知,從而引發對微觀粒子運動更精確和深入的研究,形成了量子力學這一套系統而嚴謹的學科。量子力學與對應的技術在整個20世紀飛速地發展,許許多多的科技成果與新物態發現都與量子技術息息相關,其在生活、軍事、科研等領域的應用也層出不窮。隨著量子技術的高速發展,其衍生出的不同應用領域,如量子通信、量子計算以及量子測量等領域不斷出現新的突破。其中,例如量子計算機、原子鐘等應用都在各自的領域打破了經典技術的極限,成為了前沿科技發展必不可少的技術。
正文
量子力學是由許多現代物理學家共同創立的新物理學科,是研究物質世界微觀粒子運動規律的物理學理論,主要研究原子、分子、凝聚態物質以及原子核和基本粒子的結構、性質。區別于經典力學、相對論,量子力學從根本上改變了人們對物質結構以及相互作用的理解,明確解釋了原子世界“微觀宇宙”的奇異屬性。這些基于物質微觀世界的理論催生出了量子革命,改變了世界面貌。原子彈、芯片、激光等重大發明均是來源于量子力學。量子技術作為基于量子力學發展起來的前沿技術,成為當今尖端科技中的一大熱門,發展了一系列顛覆傳統方法的新興技術。
一、量子通信
量子通信是基于量子物理的量子信息學的應用之一,因其原理上具有不可破譯特點而受到了學者們的廣泛關注。1993年美國IBM公司的研究人員首次設計了利用經典信道和量子信道(Einstein-Podolsky-Rosen, EPR糾纏態)來遠距離傳輸未知量子態的協議,后來被稱為量子隱形傳態(Quantum teleportation, QT)。1997年奧地利Anton Zeilinger小組利用獨立光子偏振態首次實現了QT實驗驗證。2022年Alain Aspect、John Clauser和Anton Zeilinger因他們在糾纏光子實驗、驗證違反貝爾不等式和開創量子信息科學方面所做出的貢獻而被授予諾貝爾物理學獎。他們各自利用糾纏量子態開展了創新性實驗,其研究結果為目前量子信息的新技術奠定了基礎。
量子通信泛指通過移動量子態實現信號、信息或量子態的傳輸和轉移的量子技術。近年來,量子通信在理論和實驗上取得了重要進展,其中量子密鑰分發(QKD)是*先走向實用化和產業化的量子信息技術,它能基于基本物理原理實現合法用戶間無條件安全的密鑰分發,是應對量子計算對傳統加密體系威脅的有效手段。
量子密鑰分發是指利用量子態來加載信息,通過一定的協議在遙遠地點的通信雙方共享密鑰。量子力學基本原理保證了密鑰的不可竊,從而在原理上實現無條件安全的量子保密通信。為實現絕對安全的保密通信,Benett與Brassard于1984年提出了首個量子密鑰分發協議,即著名的BB84協議[1]。該協議運用不確定性原理實現非正交狀態量子信息的編碼,利用光子的偏振態對密鑰進行編碼。這種方案的安全性基于量子力學的兩個基本原理:單光子的不可分割性和單光子量子態的測量塌縮性。
目前,QKD的發展重心已轉移至實用化方向。2003年由美國國防部高級研究計劃局資助的Havard大學、Boston大學和BBN科技合作建立了世界上首個量子通信網絡,后擴展為10節點量子通信網絡。2004年歐洲在維也納啟動建設基于量子加密的安全通信網絡,并于2008年建立了6節點多協議類型的8條鏈路的量子通信網絡。2010年日本在東京建立了城際高速量子保密通信網絡,并進行了一次一密的安全時頻會議應用演示。
在國內,2012年國家量子通信骨干網絡計劃即量子京滬干線在國內率先啟動QKD技術的應用,其于2017年9月正式全線開通。2017年中國科學技術大學潘建偉院士團隊利用“墨子號”量子科學實驗衛星在國際上率先成功實現了千公里級的星地雙向量子糾纏分發。此外,他們利用墨子號還實現了北京到維也納的洲際量子密鑰分發。
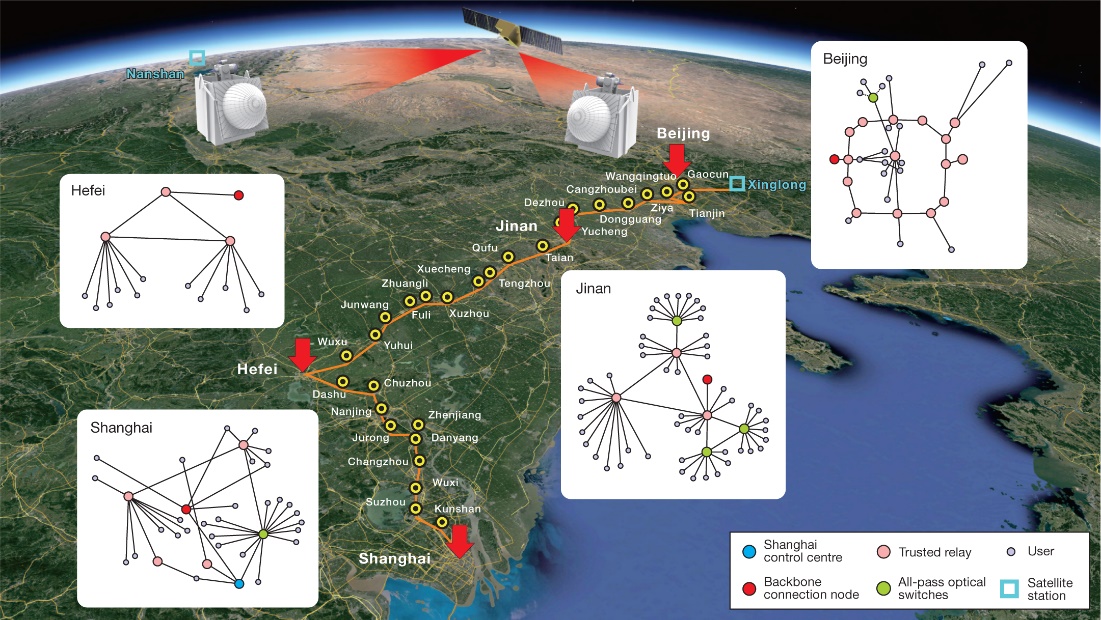
圖 1天地一體化量子網絡[2]
2021年中國科大潘建偉院士團隊在量子保密通信京滬干線與“墨子號”量子衛星成功對接的基礎上,構建了世界上首個集成700多條地面光纖QKD鏈路和兩個星地自由空間高速QKD鏈路的廣域量子通信網絡,實現了地面跨度4600公里的星地一體的大范圍、多用戶量子密鑰分發[2]。
2024年中國科學技術大學潘建偉院士團隊實現了全天候的自由空間QKD[3]。他們使用625 MHz誘騙態光源和傅里葉極限白天噪聲抑制技術,在20 km自由空間獲得了495 bps密鑰成碼率的結果。通過地基實驗在信道損耗和噪聲水平方面有效驗證了未來構建基于量子星座的星地、星間量子通信網絡的可行性,為更長的過境時間、更多的密鑰分發量和萬公里量級的量子糾纏分發提供基礎。
二、量子計算
量子計算是一種遵循量子力學規律調控量子信息單元進行計算的新型計算模式。與經典計算不同,量子計算遵循量子力學規律,它是能突破經典算力瓶頸的新型計算模式。量子計算機,作為執行量子計算任務的設備,以量子比特(qubit)為基本運算單元。在量子計算中,基于量子疊加原理,量子比特的不同狀態可被同時存儲和處理。
量子力學的基本特性是疊加態,該原理使得量子信息單元的狀態可以處于多種可能性的疊加狀態,從而導致量子計算從效率上相比于經典計算具有更大潛力。普通計算機中的2位寄存器在某一時間僅能存儲4個二進制數(00、01、10、11)中的一個,而量子計算機中的2位量子位寄存器可同時存儲這四種狀態的疊加狀態。隨著量子比特數目的增加,對于n個量子比特而言,量子信息可以處于2n種可能狀態的疊加,配合量子力學演化的并行性,可以展現比傳統計算機更快的處理速度。
量子計算的概念在80年代初期提出,并經由1985年圖靈機的概念具備了數學基本型式。而自從1994年貝爾實驗室的P. Shor證明了量子算法的實用性[4],越來越多的量子算法被提出。許多量子系統也可作為量子計算的基礎架構,例如光子偏振、腔量子電動力學和離子阱等。基于量子計算的量子計算機將大大超過傳統計算機,各國也都在致力于發展性能更好和量子位更多的量子計算平臺。
加拿大量子計算公司D-Wave于2011年正式發布全球第一款商用型量子計算機D-Wave,開啟量子計算機的熱潮。并在2017年推出D-Wave 2000Q,超越經典的專業算法1000-10000倍。而與此同時算法也在不斷的更替,從早期的Shor和Grover算法,逐漸發展到尋找*優解,收斂速度更快的HHL、QAOA和F-VQE等算法[5]。
近年來,量子計算產業鏈和應用以各互聯網企業為核心進行發展。國外方面,IBM、谷歌、微軟、霍尼韋爾和亞馬遜等互聯網企業均在量子計算領域有所布局,開展了量子計算的全面研發,包括硬件、算法以及軟件等。IBM基于超導路線已研發127量子比特處理器“Eagle”,推出開源Qiskit Metal量子軟件;谷歌研制成功53量子比特計算機“懸鈴木”,擁有TensorFlow-Quantum和FermiNet等多款應用軟件。此外,D-Wave、IonQ和Regetti Computing等企業也在積極投入量子計算研發。并且量子技術已上升至國家技術層面,如美國國防部(DAPRA)和歐盟都制定了國家級別的量子技術戰略目標布局計劃,俄羅斯和日本也在陸續啟動多項規劃。
國內在量子計算方面也取得了全球矚目的成就。2021年中科院潘建偉團隊通過超導路線對量子比特進行調控,先后研制成功62位可編程超導量子計算機原型“祖沖之號”,如圖 2左圖所示;以及66位“祖沖之二號”;經評估,其采樣復雜程度超越谷歌“懸鈴木”2-3個數量級。而利用室溫下即可實現的光量子路線,中科大研究團隊于2020年成功構建76個光子的“九章”量子計算原型機,如圖 2右圖所示,并在次年突破至113個光子,比超級計算機速度快1024倍。2018年,華為公布了量子計算模擬器HiQ云服務平臺;2020年百度也推出了百度量子平臺,并在2022年發布了產業級超導量子計算機“乾始”。量子計算以其遠超傳統計算機的速度,將在數字信號處理、軍事智能、物流管理等需要強大計算能力的領域大展宏圖。

圖 2 “祖沖之號”量子處理器(左)“九章”光量子干涉實物圖(右)圖源:維基百科
三、量子模擬
1982年,在費曼的一次演講"Simulating physics with computers"中[6],首次明確提出了量子模擬的概念。他指出,由于在量子力學系統中基的空間隨粒子數目呈指數增長,經典計算機很難解決此類問題。一種可行的解決方法是"A quantum for a quantum",即通過量子系統來“模擬”量子系統。這也就是量子模擬的基本思想。量子模擬器會通過構造與目標體系等效的哈密頓量來模擬對應的系統,給出定量或定性的結論。
冷原子是一類非常重要的量子模擬體系,由于其易于操控和測量的特點,可用于多種物理體系的構建。冷卻至低溫的玻色子與費米子展現出了良好的量子簡并性,在Feshbach共振下,可對原子間的散射長度進行較為自由的調節,這對于研究多體與少體相互作用的物理機制有著重要的意義。
關于Feshbach共振對量子系統的調控,Yoshiro Takahashi等人成功實現了亞微米空間尺度的Feshbach共振調控,并利用衍射圖樣擬合了散射長度的大小[7]。散射長度的空間調制證明了原子相互作用的高分辨率控制是可能的,該靈活性也說明了可以利用量子系統進行模擬。
Gustavsson等人展開了玻色-愛因斯坦凝聚態(BEC)原子的Bloch振蕩的研究[8],他們利用Feshbach共振將原子間相互作用調至0,在這樣的條件下觀察到了超過2萬次的Bloch振蕩,能夠在無相互作用的極限下實現基于BEC的原子干涉儀。
國內關于Feshbach共振的研究也有許多,例如張婧、李東豪教授小組在實驗上成功實現了p波Feshbach共振技術,利用激光實現束縛態的躍遷[9],如圖 3所示。而在聶亮、張越等人的工作中,成功實現了同核和異核Feshbach共振,為模擬量子流體等相互作用提供了理想的平臺[10]。
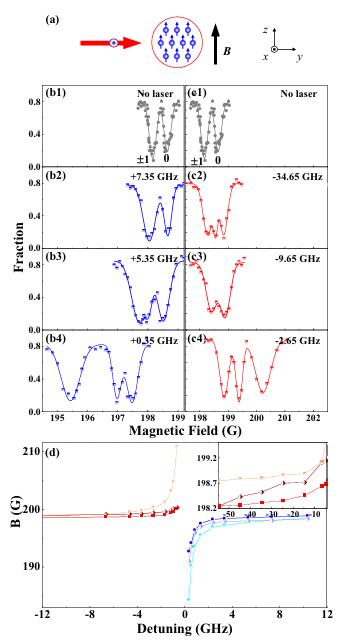
圖 3 由光場驅動的p波Feshbach共振[10]
光晶格則使得冷原子量子模擬的對象大大增加,通過構造周期性勢場,可以對多種格點體系進行模擬,如圖 4所示[11]。晶格中這種超冷原子的相互作用由Hubbard模型給出。Hubbard模型是一種基本的量子模型,可對磁性和超流等現象有所解釋。目前的冷原子實驗已能夠實現低溫下Hubbard模型中的多種相變。此外,目前人們也正在嘗試在冷原子系統中構建人造規范勢,從而模擬具有規范荷(如電荷)的體系,通過這種方法揭示量子霍爾效應、拓撲絕緣體等現象的內在機制。
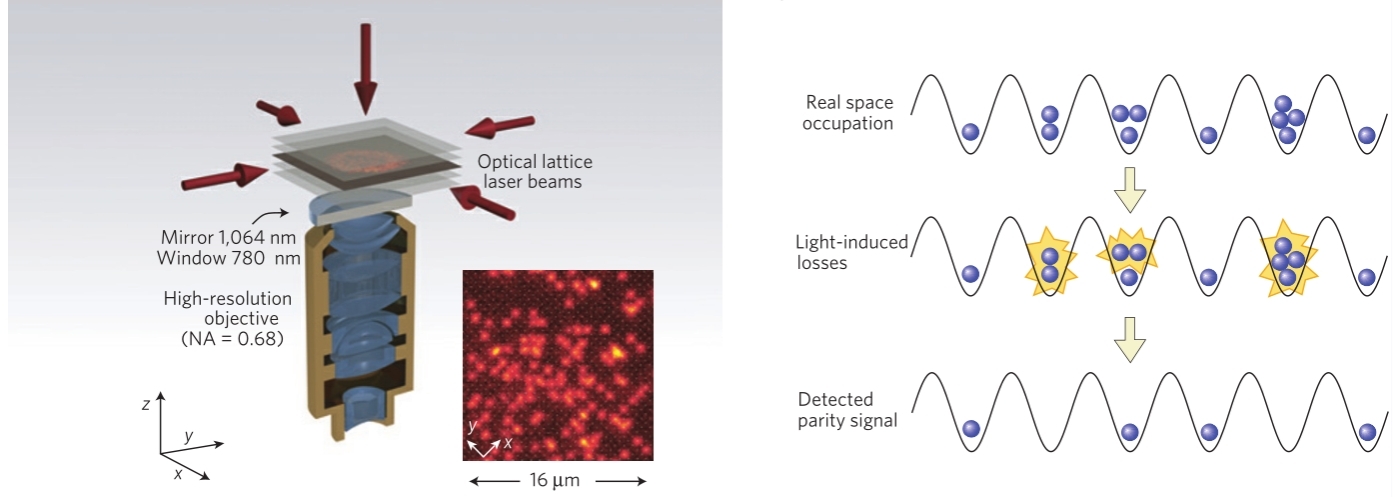
圖 4 光晶格中的超冷原子[11]
Immanuel Bloch等人研究了光晶格中冷原子的相變[12]。由Hubbard模型給出,相鄰格點的跳變由隧道耦合能和各點相互作用能表征,對于排斥性的玻色子,利用晶格深度的增加,相互作用達到某一臨界強度時,系統會經歷由超流體轉變為Mott絕緣態的相變。
而光學晶格量子模擬中*活躍的問題之一就是Fermi-Hubbard模型的實現[13],可為材料的電子和磁性提供重要依據。而將費米量子氣體加載進光晶格中的實現,讓Fermi-Hubbard模型成為可能。這樣的Fermi-Hubbard模型中,哈密頓量由干涉激光場和超冷原子碰撞產生,給予途徑模擬哈密頓量,并能夠解決許多多體系統的開放問題。
而除了光晶格系統中的Hubbard模型,還存在其它模型,例如伊辛模型。伊辛模型是描述物質鐵磁相變的重要模型,而量子系統在模擬一維和二維伊辛模型上均有重要進展。2023年,IBM團隊利用127比特的量子系統實現了對超過100個自旋的二維橫向伊辛場模型的動力場模擬,超越了經典近似方法模擬的計算精度,之后可進一步走向實用化。
量子模擬還可以解決拓撲物理系統和其他多體問題。拓撲物理是凝聚態物理研究的重要方向之一,理解物質的拓撲性質有助于研究更為穩定的拓撲量子計算機。目前,超導量子計算機已經可以模擬各類物理模型中的拓撲物理性質:比如一維超導模型Kitaev鏈的拓撲相變的模擬;利用變分能量求解算法,實現對二維超導體波函數拓撲不變量,包括陳數,幾何相變的模擬;模擬二維陳絕緣體能帶、拓撲零能模和拓撲非平庸邊緣態等。此外,在模擬流體力學系統、天體物理與高能物理系統等方面均是量子模擬可應用的方向。近年來,基于超冷原子的量子模擬取得了巨大的進展,徹底改變了我們探測微觀系統的方式,通過精密的原子操控,能夠實現對多體系統的高還原度模擬,為各領域的理論預言和實驗驗證提供有效的手段。
四、量子測量
量子測量是量子力學*基本和核心的問題之一。經典物理中的測量過程為對被測者不加改變的提取,然而在量子體系中,根據馮·諾依曼的測量假定,量子測量會導致量子態塌縮至待測物理量的本征態,即不同于經典測量,量子測量會對被測系統產生影響,相同的量子系統被測量后可能會獲得完全不同的結果,而這些結果將符合一定的概率分布。
量子測量基于微觀粒子量子態精密測量,完成被測系統物理量的執行變換和信息輸出,在測量精度、靈敏度和穩定性等方面與傳統測量技術相比有明顯優勢。在量子測量方面,目前已經研發并攻克了多項技術,例如原子的激光冷卻與俘獲技術、原子噴泉技術和物質波干涉操控技術等關鍵技術。通過這些技術而實現的量子測量,可以了解量子的物理狀態和原子微觀性質,從而更好地對其進行應用。原子干涉儀,原子陀螺儀,原子鐘等均是量子測量領域代表性成果。
4.1 原子干涉儀
1924年德布羅意首次提出了粒子的波動特性,粒子的波長由粒子的動量決定,物質波是量子力學理論的基本概念之一。物質波干涉技術在此理論基礎上發展起來,隨著對原子結構及其物理性質的理解,利用原子干涉技術進行引力測量的實驗也逐步被實現。
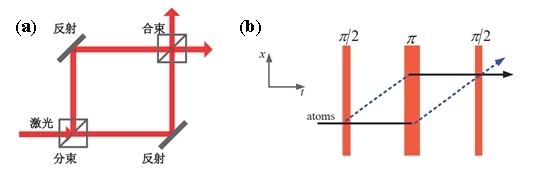
圖 5 (a)Mach-Zehnder光學干涉儀示意圖 (b)三脈沖原子干涉儀示意圖
Mach-Zehnder光學干涉儀原理圖如圖 5(a)所示,從光源發出激光經分束鏡后分成兩束,兩束激光經過不同的路徑分別被不同反射鏡反射,再一次經過分束鏡時發生干涉,*后通過探測器讀出干涉信號后可得到相關相位信息。在光學干涉儀中,激光攜帶被測量的相位信息,而分束器和反射鏡改變光的路徑,激光的動量在被物質吸收和再反射時發生變化。原子干涉儀的工作原理與Mach-Zehnder光學干涉儀類似,而原子干涉儀將原子作為物質波,光脈沖作為光學元件,獲得的相位差包含原子經歷外場的所有信息,如重力加速度、重力梯度、地球轉動和磁場等。
目前各種各樣的原子干涉實驗正利用原子的波動特性進行精密測量和量子力學基本原理的檢驗。原子干涉儀具有較高的靈敏度和很好的長期穩定性,比較常用的原子干涉儀可分為原子干涉重力儀、原子干涉梯度儀和原子干涉陀螺儀等。可用于重力加速度測量、重力梯度測量和引力場曲率測量、萬有引力常數測量、地球轉動測量、精細結構常數測量、微觀距離下的引力研究以及暗物質探測等。還可比較不同重力原子的自由下落以及不同自旋方向、不同超精細能態的原子來檢驗廣義相對論中的弱等效原理。此外,還可在空間中用原子干涉儀探測引力波。目前,利用原子干涉儀進行高精度重力測量的實驗以達到了4.2 μGal rad/s/Hz1/2的短期靈敏度[14],利用原子干涉儀進行弱等效原理檢驗的實驗已經達到了10-12的較高水平[15]。
4.2 原子陀螺
陀螺儀可提供全自主、實時、連續的導航技術,成為實現高精度無縫導航的關鍵技術。慣性導航陀螺儀可分為光學陀螺儀、微機電陀螺儀與原子陀螺儀等。
利用堿金屬原子的進動測量磁場大小可實現磁力計,提高原子磁力計的靈敏度可研制高性能的原子陀螺儀。原子陀螺儀根據工作原理不同可分為原子自旋式陀螺儀以及原子干涉式陀螺儀等,其中原子自旋式陀螺儀包括無自旋交換弛豫(Spin exchange relaxation free, SERF)陀螺儀、核磁共振(Nuclear magnetic resonance gyroscope, NMRG)陀螺儀等。陀螺儀中的角度隨機游走(Angle random walk, ARW)和漂移穩定性(Bias stability)是表征其性能的兩個主要指標。相較于光學陀螺儀和微機電陀螺儀,原子陀螺儀具有精度高、體積小且對加速度不敏感的優點。
4.2.1 無自旋交換弛豫陀螺儀
SERF原子自旋陀螺儀利用電子自旋敏感物體轉動,具有精度高、體積小的特點。其主要工作過程為原子SERF態制備以及原子自旋進動檢測。其工作原理如圖 6所示,磁屏蔽裝置使原子處于近零磁場環境中,此時堿金屬原子的拉莫爾進動頻率大幅降低,同時由于高密度高壓環境使自旋交換率極大提升,從而充分抑制原子的自旋交換弛豫,實現SERF態。當載體轉動時,由于電子自旋的定軸性,檢測激光與電子自旋產生的宏觀磁矩M間存在夾角α,通過檢測該角度即可得到載體轉動信息。
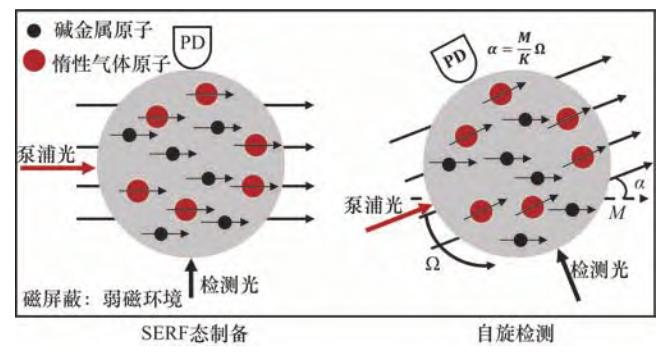
圖 6 無自旋交換弛豫陀螺工作原理[16]
21世紀初普林斯頓大學Romalis首次實現了基于SERF效應的超高靈敏度原子磁強計[17],2018年普林斯頓Romalis團隊和Twinleaf公司使用87Rb磁強計抑制Rb原子之間的自旋交換弛豫,在直徑10 mm的氣室下,實現了角度隨機游走0.025°/h1/2,零偏穩定性優于0.01°/h的SERF陀螺儀。北京航空航天大學房建成院士團隊在2008年率先開展基于原子自旋的超高靈敏度磁場測量與慣性測量技術研究,在2018年研制了零偏穩定性優于0.05 °/h的雙軸SERF陀螺,在2019年研制出小型化SERF陀螺原理樣機,在2020年陀螺儀原理樣機的零偏穩定性達到0.001 °/h量級[18]。
4.2.2核磁共振陀螺儀
NMRG陀螺儀利用磁場中原子核自旋的進動即拉莫爾進動來測量旋轉[19],兼顧低功耗、體積小、低成本、高精度和抗振動等綜合優勢,目前發展較為成熟。在核磁共振陀螺中,原子核自旋可以在慣性空間中保持其原始指向,所以可以用原子核自旋對轉動的敏感研制核磁共振陀螺儀,其裝置原理圖如圖 7所示。
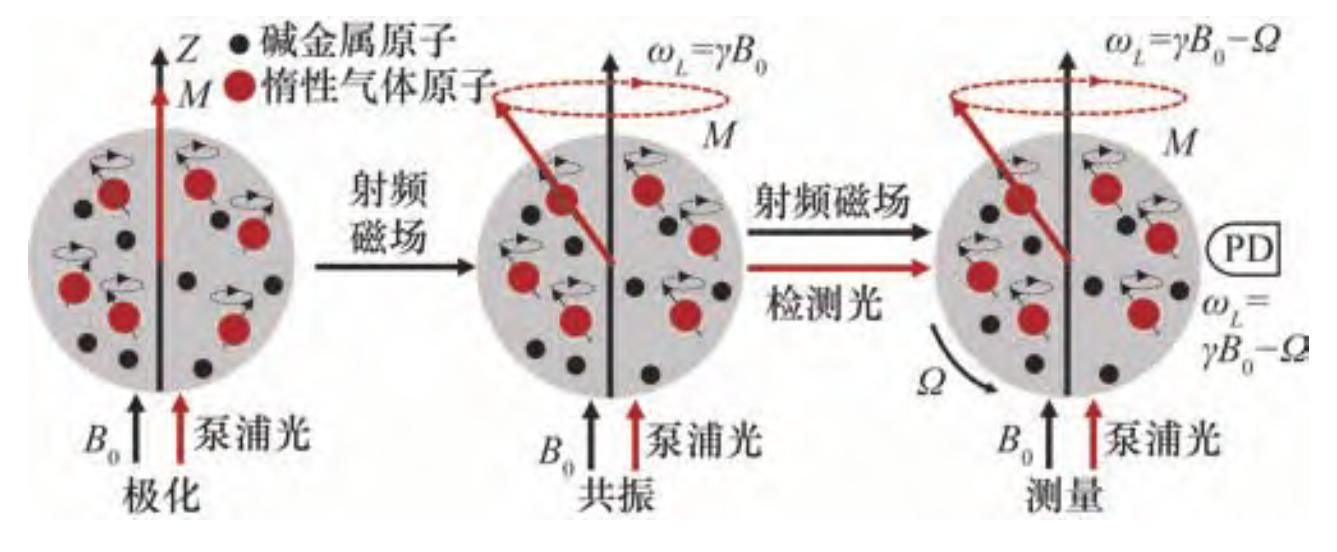
圖 7 核磁共振陀螺儀原理示意圖[16]
原子核自旋具有磁矩μ,取向與自旋軸方向一致,在自然狀態下具有隨機性,無宏觀指向,將核自旋置于靜磁場?0中,核自旋將在靜磁場作用下以拉莫爾角頻率繞?0方向進動。在此基礎上,作用與磁場?0方向相同的泵浦光后,可使得原子被極化,賦予核自旋宏觀指向。通過在正交于已有穩定靜磁場?0方向外加頻率與原子進動頻率相等均勻的交變電磁場?1(?),核自旋會產生核磁共振,且共振頻率等于拉莫爾角頻率。探測光與載體固定并且隨其共同旋轉,探測光檢測宏觀核自旋的拉莫爾進動頻率,能夠獲得載體旋轉的角速度,也可計算求解靜磁場?0的大小
20 世紀50 年代,構建核磁共振陀螺儀實現轉動測量的想法被第一次提出[20]。隨后在20 世紀60 年代,直接使用光抽運汞的核磁共振陀螺儀被制造出來。隨后20 年,基于汞元素的核磁共振陀螺儀的角度隨機游走可達到0.05 °/h1/2,漂移穩定性則為0.02 °/h[21]。此外,我國北京自動化控制設備研究所、北京航空航天大學、北京航天控制儀器研究所、華東師范大學和西安飛行自動控制研究所等單位對核磁共振陀螺儀現階段的重要問題進行了深入的研究和探索,如核磁共振陀螺儀的磁屏蔽性能優化、用來測量核自旋進動頻率的堿金屬原子磁力計的靈敏度、系統誤差來源的研究、磁場模塊的優化設計和抽運光頻率的影響以及激光頻率鎖定等關鍵科學與技術問題方面都取得顯著進展。4.2.3 原子干涉陀螺儀
原子干涉陀螺儀的原理與光學干涉陀螺儀類似,利用了原子作為物質波的波動性,基于Sagnac效應完成角速度的測量。原子干涉陀螺儀工作過程主要包含原子團制備、原子分束、原子反射、原子合束和干涉相位測量,其基本原理如圖 8所示。原子束中的原子經內態選擇后全部處于基態,然后經拉曼光脈沖分別實現分束、反射和合束,*后通過干涉條紋的相位測量獲取轉動信息。
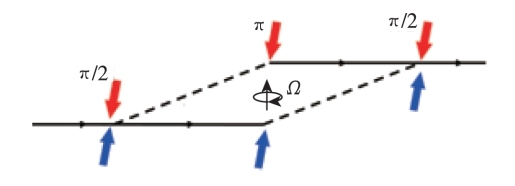
圖 8受激拉曼躍遷和原子干涉陀螺原理圖
隨著激光冷卻原子技術的發展,第一個脈沖型冷原子干涉陀螺儀于2003年由法國巴黎天文臺Landragin小組實現[22]。2018年,該小組實現了首個零偏不穩定性低于1nrad/s的原子干涉陀螺儀,其短期靈敏度為3×10-8 rad/s/Hz1/2,零偏不穩定性為3.0×10-10 rad/s@4000s[23]。2022年中國科學院精密測量科學與技術創新研究院采用冷原子雙平拋方案,靈敏度為1.5×10-7 rad/s/Hz1/2,零偏不穩定性為9.5×10-9 rad/s@20000s[24]。近年來,原子干涉陀螺儀逐漸從實驗室環境走向工程應用,這一過程中還有許多問題亟待解決。其中,既有保持精度前提下的集成化、小型化和提高系統魯棒性與自動化程度的工程技術問題,也有提高數據更新率、帶寬和動態范圍的基礎技術問題,后者是制約目前原子干涉陀螺儀動態環境應用的瓶頸技術問題。
4.3 原子鐘
時間是描述事件發生前后序列的物理量。隨著精密計時工具的發明,天文秒不是恒定不變的。量子力學的建立和發展使科學家認識到原子內部電子能級間的特征躍遷頻率具有比天文現象更高的穩定度,不隨時間和地點的變化而變化,更適用于作為時間標準,從而產生了原子鐘。由原子鐘生成的秒,稱為“原子秒”。

圖 9 原子鐘基本原理示意圖
原子鐘的工作原理如圖 9所示,使用本振源(晶振或者超穩頻率源)的標準頻率。一路作為輸出,另一路通過頻率綜合器得到特定頻率數值輸出原子鐘躍遷頻率。將此頻率信號作用于原子系綜,使原子發生能級躍遷,利用躍遷幾率作為誤差信號反饋至本振源,*終將本振源的頻率鎖定到原子躍遷頻率上。
1955年,英國國家物理實驗室研制成國際上第一臺銫原子鐘[25]。1967年第13屆國際計量大會將秒定義在銫133原子在無外界干擾的條件下基態兩個超精細能級間躍遷對應的輻射頻率上。2018年國際計量大會基于常數的新理念重新表述了秒定義:當銫133原子基態的超精細能級躍遷頻率以單位Hz表示時,將其固定數值取為9 192 631 770來定義秒[26]。
光學原子鐘(光鐘)則是利用頻率在光學波段的原子(分子、離子)躍遷作為量子參考而建立的原子鐘。根據對量子參考躍遷對象的不同,光鐘可分為離子光鐘、光晶格鐘和核光鐘等。離子光鐘采用了離子阱技術,利用磁場、靜電場或射頻場將帶電離子囚禁在超高真空中,離子與外界環境較好地隔離,具有系統頻移不確定度低的優點,目前世界上*好的離子光鐘的系統頻移不確定度已進入10-19量級,但是由于目前的離子光鐘只囚禁了一個離子,因此受到量子投影噪聲限制,使得頻率穩定度差于囚禁多個參考粒子的中性原子光鐘。中性原子光晶格鐘利用光晶格囚禁大量中性原子作為量子參考,通過光晶格把原子囚禁在Lamb-Dicke區域,消除運動效應(熱運動和光子反沖)造成的影響,同時引入“魔術波長”光晶格技術,減小由于光晶格激光的引入而造成的系統頻移,增加原子與鐘躍遷探測激光的作用時間,減小探測的傅里葉極限線寬,實現了1秒平均頻率穩定度進入10-17量級。

圖 10 光學原子鐘實物 圖源:JILA
全世界范圍內多家單位都在不斷提高和突破相關技術以實現更高精度的光鐘,國內外主要有171Yb鐿光晶格鐘、87Sr鍶光晶格鐘和離子光鐘等。在中性原子光晶格鐘方面,美國實驗室天體物理聯合研究所(Joint Institute for Laboratory Astrophysics, JILA)葉軍教授小組在2022年實現了在單個真空腔內利用87Sr鍶原子分辨微米量級重力紅移[27],有力地證明了光鐘在頻率計量上的超高分辨特性;他們在2024年首次將光晶格中的原子制備在Wannier-Stark本征態上,獲得創記錄的相干時間;并精密控制碰撞頻移、晶格光頻移,以及使用對磁場*不敏感的鐘躍遷,評估87Sr鍶光晶格鐘不確定度為8.1×10-19,正式將光晶格鐘的不確定度推進10-19量級[28]。美國國家標準與技術研究所(National Institute of Standards and Technology, NIST) A. D. Ludlow小組在2018年報道了使用輻射屏蔽腔降低Zeeman頻移和黑體輻射頻移不確定度,評估171Yb鐿原子光鐘不確定度為1.4×10-18[29]。在離子光鐘的不穩定度和不確定度報道方面,NIST的D. R. Leibrandt小組在2019年報道了27Al+鋁離子量子邏輯光鐘,他們使用新研制的離子阱抑制27Al+鋁離子熱運動,測得27Al+鋁離子光鐘的不穩定度和不確定度分別為1.2×10-15/√?和9.4×10-19[30]。中國科學院精密測量科學與技術創新研究院(Innovation Academy for Precision Measurement Science and Technology, APM)高克林教授小組在2022年報道了液氮制冷下不確定度為3×10-18[31]的40Ca+鈣離子光鐘。除了光晶格鐘和單離子鐘等光鐘外,也有不少研究單位研制出分子光鐘[32]、高價離子鐘[33]和核光鐘[34]等。
結論
量子力學的提出是一里程碑式的人類認知的突破,往后幾乎所有偉大的科學發現都和量子技術密不可分。而隨著量子技術在量子通信、量子計算、量子測量等領域的不斷發展,量子技術的進一步突破已引起人們越來越多的關注。近年來,量子技術領域方興未艾,其催生的技術變革以及應用發展正在改變世界面貌,成為了諸多前沿領域發展的基石。由于這些技術影響到社會、軍事、科技、經濟等多方面,各國也都將量子技術的發展定為重大戰略目標。量子技術持續不斷的突破讓科學發展生機勃勃,其發展前景和對未來技術的影響將不可限量,并必將引領新一輪科技革命和產業變革。
作者簡介
第一作者:金濤韞、彭成權
通訊作者:徐信業 教授
作者單位:華東師范大學精密光譜科學與技術國家重點實驗室
引用文獻
1. Bennett, C.H. and G. Brassard. Quantum cryptography: Public key distribution and coin tossing. in IEEE International Conference on Computers, Systems and Signal Processing. 1984.
2. Chen, Y.-A., et al., An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature, 2021. 589(7841): p. 214-219.
3. Cai, W.-Q., et al., Free-space quantum key distribution during daylight and at night. Optica, 2024. 11(5): p. 647-652.
4. Shor, P.W. Algorithms for quantum computation: discrete logarithms and factoring. in Proceedings 35th Annual Symposium on Foundations of Computer Science. 1994.
5. Amaro, D., et al., A case study of variational quantum algorithms for a job shop scheduling problem. EPJ Quantum Technology, 2022. 9(1): p. 5.
6. Feynman, R.P., Simulating physics with computers, in Feynman and computation. 2018, CRC Press. p. 133-153.
7. Yamazaki, R., et al., Submicron spatial modulation of an interatomic interaction in a Bose-Einstein condensate. Physical Review Letters, 2010. 105(5): p. 050405.
8. Gustavsson, M., et al., Control of Interaction-Induced Dephasing of Bloch Oscillations. Physical Review Letters, 2008. 100(8): p. 080404.
9. Peng, P., et al., Universal feature in optical control of a p-wave Feshbach resonance. Physical Review A, 2018. 97(1): p. 012702.
10. 聶亮, et al., ~(39)K-~(87)Rb雙組分|F=1,m_F=-1>態玻色-愛因斯坦凝聚體的實驗制備. 量子光學學報, 2022. 28(03): p. 215-222.
11. Bloch, I., J. Dalibard, and S. Nascimbene, Quantum simulations with ultracold quantum gases. Nature Physics, 2012. 8(4): p. 267-276.
12. Greiner, M., et al., Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature, 2002. 415(6867): p. 39-44.
13. Esslinger, T., Fermi-Hubbard physics with atoms in an optical lattice. Annu. Rev. Condens. Matter Phys., 2010. 1(1): p. 129-152.
14. Hu, Z.-K., et al., Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Physical Review A, 2013. 88(4): p. 043610.
15. Asenbaum, P., et al., Atom-interferometric test of the equivalence principle at the 10− 12 level. Physical Review Letters, 2020. 125(19): p. 191101.
16. 駱曼箬, et al., 原子陀螺研究進展及展望. 測控技術, 2023. 42(10): p. 1-10.
17. Allred, J., et al., High-sensitivity atomic magnetometer unaffected by spin-exchange relaxation. Physical review letters, 2002. 89(13): p. 130801.
18. Fu, Y., et al., Effects of probe laser intensity on co-magnetometer operated in spin-exchange relaxation-free regime. IEEE Transactions on Instrumentation and Measurement, 2022. 71: p. 9501607.
19. Donley, E.A. Nuclear magnetic resonance gyroscopes. in SENSORS, 2010 IEEE. 2010. IEEE.
20. Leete, B.D., Apparatus for measuring angular motion. 1955, Google Patents.
21. Karwacki, F., Nuclear magnetic resonance gyro development. Navigation, 1980. 27(1): p. 72-78.
22. Yver-Leduc, F., et al., Reaching the quantum noise limit in a high-sensitivity cold-atom inertial sensor. Journal of Optics B: Quantum and Semiclassical Optics, 2003. 5(2): p. S136.
23. Savoie, D., et al., Interleaved atom interferometry for high-sensitivity inertial measurements. Science advances, 2018. 4(12): p. eaau7948.
24. Yao, Z.-W., et al., Self-alignment of a large-area dual-atom-interferometer gyroscope using parameter-decoupled phase-seeking calibrations. Physical Review A, 2021. 103(2): p. 023319.
25. Essen, L. and J.V. Parry, An atomic standard of frequency and time interval: a caesium resonator. Nature, 1955. 176(4476): p. 280-282.
26. Milton, M., On the revision of the International System of Units (SI). Draft Resolution A, 2018.
27. Bothwell, T., et al., Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature, 2022. 602(7897): p. 420-424.
28. Aeppli, A., et al., A clock with 8×10-19 systematic uncertainty. arXiv preprint arXiv:2403.10664, 2024.
29. McGrew, W., et al., Atomic clock performance enabling geodesy below the centimetre level. Nature, 2018. 564(7734): p. 87-90.
30. Brewer, S.M., et al., 27Al+ quantum-logic clock with a systematic uncertainty below 10-18. Physical Review Letters, 2019. 123(3): p. 033201.
31. Huang, Y., et al., Liquid-nitrogen-cooled Ca+ optical clock with systematic uncertainty of 3×10-18. Physical Review Applied, 2022. 17(3): p. 034041.
32. Leung, K., et al., Terahertz vibrational molecular clock with systematic uncertainty at the 10-14 level. Physical Review X, 2023. 13(1): p. 011047.
33. King, S.A., et al., An optical atomic clock based on a highly charged ion. Nature, 2022. 611(7934): p. 43-47.
34. Peik, E., et al., Nuclear clocks for testing fundamental physics. Quantum Science and Technology, 2021. 6(3): p. 034002.
免責說明
北京卓立漢光儀器有限公司公眾號所發布內容(含圖片)來源于原作者提供或原文授權轉載。文 章版權、數據及所述觀點歸原作者原出處所有,北京卓立漢光儀器有限公司發布及轉載目的在于傳遞 更多信息及用于網絡分享。
如果您認為本文存在侵權之處,請與我們聯系,會第一時間及時處理。我們力求數據嚴謹準確, 如有任何疑問,敬請讀者不吝賜教。我們也熱忱歡迎您投稿并發表您的觀點和見解。