日本韩国欧美,三年在线观看免费观看完整版中文,久久精品无码鲁网中文电影,日本理伦年轻的妻子

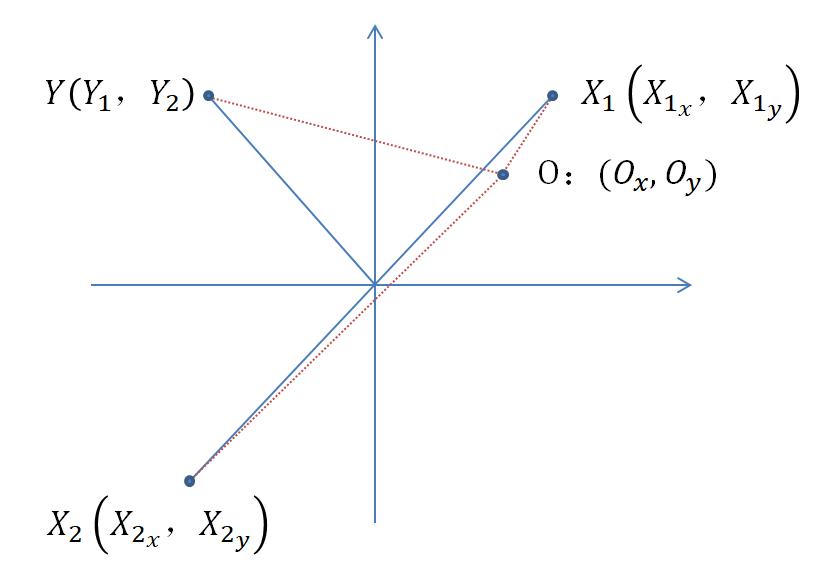
運動學正解：可變端→終端）

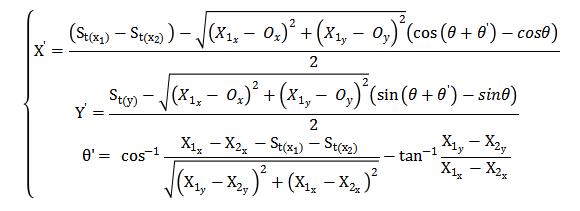
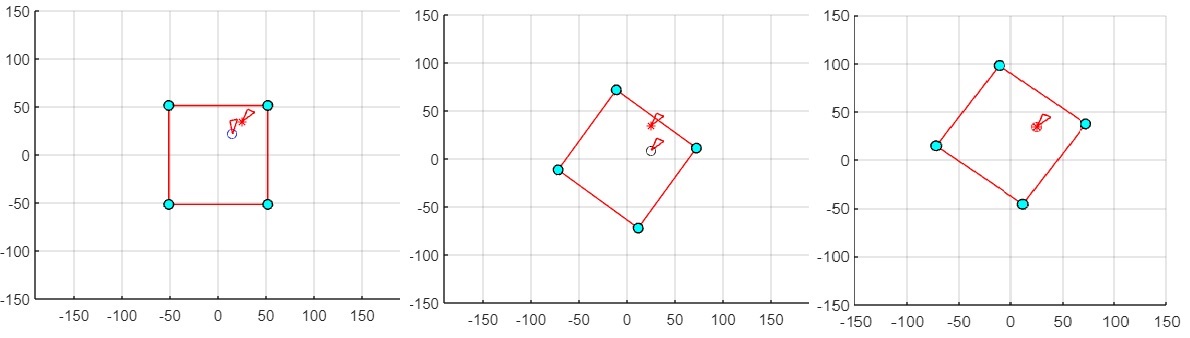
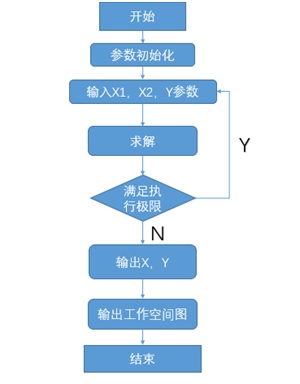
對位平臺的工作空間求解

工作空間指在一定條件下，終端執行器所能到達的空間位置的集合。一般來說，并聯結構的工作空間都比較小，所以在一定程度上限制了其應用。因此對于并聯結構的工作空間進行分析就顯得尤為重要。

對于工作空間的求解一般采用解析法或數值法，解析法從工程角度而言十分繁瑣，直觀性不強；數值法利用位置正解或逆解來求解工作空間。我們通過MATLAB軟件求解機構的位置正解及電機和導軌行程作為限制條件進行工作空間的求解。

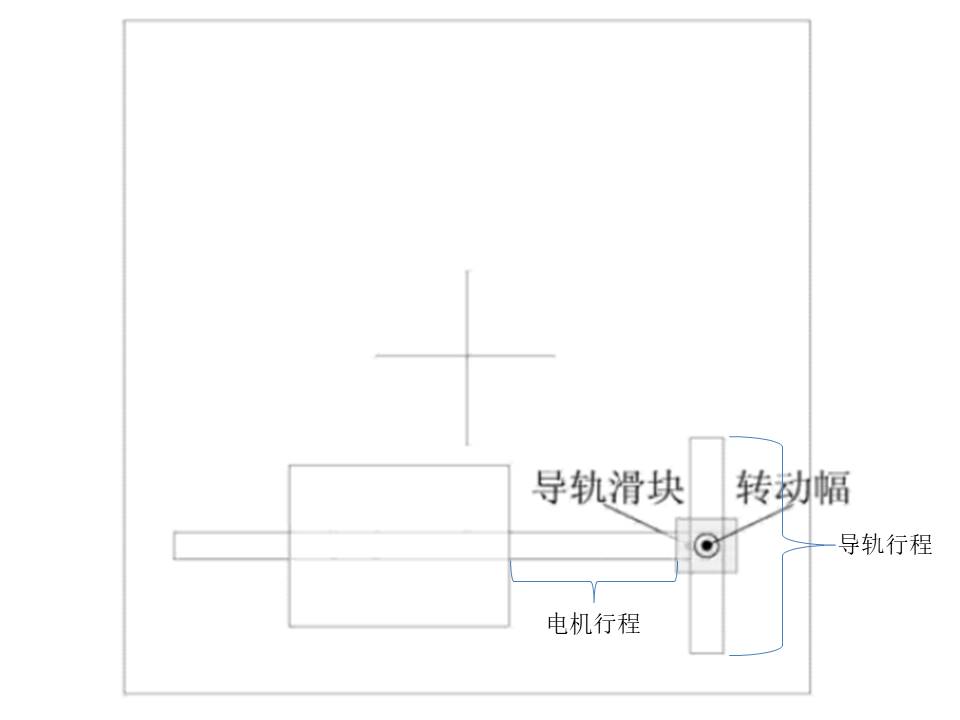
定義平臺結構參數：X1 = X2 = Y = 137.89mm，電機行程范圍：-15mm ≤ (x1 = x2 = y) ≤ 15mm，導軌行程：-15mm ≤ d ≤ 15mm。

工作空間仿真圖

Matlab部分代碼參考：

close all; clear all; clc

%% 設置模板位置參數

figure(1)

grid on;axis([-200,200,-200,200]);hold on;

% 定義生成模板物體mode:x,y,theta（基于XYR平臺絕對坐標系）

Template = [25, 35 , pi*0.2];

% 定義待糾偏物體re:x,y,theta（基于XYR平臺絕對坐標系）

Rectify_deviation = [15, 22, pi*0.4];

% Y軸執行機構-目標坐標

yx = (Yx0 - at)*cos(THETA) - (Yy0 - bt)*sin(THETA) + at + X;

yy = (Yx0 - at)*sin(THETA) + (Yy0 - bt)*cos(THETA) + bt + Y;

% X1軸執行機構-目標坐標

x1x = (X1x0 - at)*cos(THETA) - (X1y0 - bt)*sin(THETA) + at + X;

x1y = (X1x0 - at)*sin(THETA) + (X1y0 - bt)*cos(THETA) + bt + Y;

% X2軸執行機構-目標坐標

x2x = (X2x0 - at)*cos(THETA) - (X2y0 - bt)*sin(THETA) + at + X;

x2y = (X2x0 - at)*sin(THETA) + (X2y0 - bt)*cos(THETA) + bt + Y;

% O坐標

ox = (Ox0 - at)*cos(THETA) - (Oy0 - bt)*sin(THETA) + at + X;

oy = (Ox0 - at)*sin(THETA) + (Oy0 - bt)*cos(THETA) + bt + Y;

%求出第一次旋轉后，待糾偏物體新的位姿

rx1 = Rectify_deviation(1);

rx2 = Rectify_deviation(2);

Rectify_deviation(1) = (rx1 - at)*cos(THETA) - (rx2 - bt)*sin(THETA) + at + X;

Rectify_deviation(2) = (rx1 - at)*sin(THETA) + (rx2 - bt)*cos(THETA) + bt + Y;

Rectify_deviation(3) = Rectify_deviation(3) + THETA_M;       PX(incr)=-sin(Theta1).*(d2+sin(Theta4).*sin(Theta5).*d6)+cos(Theta1).*(cos(Theta2).*cos(Theta4)*sin(Theta5)*d6+sin(Theta2)*(d3+cos(Theta5)*d6));          PY(incr)=cos(Theta1).*(d2+sin(Theta4).*sin(Theta5).*d6)+sin(Theta1).*(cos(Theta2).*cos(Theta4)*sin(Theta5)*d6+sin(Theta2)*(d3+cos(Theta5)*d6));

PZ(incr)=-cos(Theta4)*sin(Theta2)*sin(Theta5)*d6+cos(Theta2)*(d3+cos(Theta5)*d6);

以對位臺面重心為參照點，則有：